react-spring: Interpolation
react-spring에서 등장하는 interpolation이 무엇인지 간단하게 알아보자.
글을 시작하기에 앞서, 필자는 그래픽, 통계, 컴퓨터 관련 전공이 아니기 때문에 설명이 정확하지 않을 수 있다. 하지만 interpolation이 대충 무엇인지 파악하는데는 충분할 거라 믿는다.
Interpolation 단어적 의미
interpolation을 구글에 치면 가장 먼저 나오는 것이 '선형 보간법(linear, bilinear, trilinear interpolation)'이 나온다.
우선 이 글에서는 linear interpolation(선형 보간법)만 다루겠다.
선형은 직선이란 뜻이다.
그렇다면 보간법이 무엇일까?
국립국어원 표준국어대사전을 보면 '(수학) 둘 이상의 변숫값에 대한 함숫값을 알고서, 그것들 사이의 임의의 변숫값에 대한 함숫값이나 그 근삿값을 구하는 방법'을 뜻한다.
더 쉽게 보자면, 아래의 그림에서 p1과 p2 사이에 있는 점 p의 값을 추정하기 위해 '선형 보간법'을 사용할 수 있다.
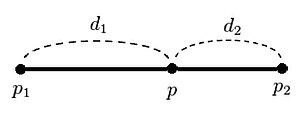
https://ko.wikipedia.org/wiki/%EC%84%A0%ED%98%95_%EB%B3%B4%EA%B0%84%EB%B2%95
해당 그림에서 점 p를 구하는 공식은 아래와 같다.
https://ko.wikipedia.org/wiki/%EC%84%A0%ED%98%95_%EB%B3%B4%EA%B0%84%EB%B2%95
회귀와 보간의 차이점
회귀(regression)도 주어진 데이터로 어떤 값을 추정하는 것이지만, 회귀는 기존 데이터에 오차가 있다고 가정하여 오차범위를 생각하여 범위를 return한다.
하지만 보간(interpolation)은 기존 데이터가 정확한 데이터라 가정하기 때문에 결과값이 값으로 나온다.
언제 interpolation을 사용하는가?
이렇게만 보면 언제 사용되는지 잘 모를 수 있다. 우리가 interpolation을 가장 많이 체감할 수 있는건 사진이다.
위 짤처럼, 사람들이 퍼가다보면 사진 화질이 안좋아져서 확대하면 흐릿하게 보인다. 이때 우리는 주로 '픽셀(px)이 깨졌다'라고 표현한다.

https://twlab.tistory.com/23
해상도가 매우 높아 우리 눈에는 공백이 없는 사진처럼 보여도, 컴퓨터는 컴퓨터가 찾을 수 있는 가장 작은 단위의 px로 저장하기 때문에 확대를 하면 공백이 있을 수 밖에 없다.
그리고 이 공백을 주변의 px값에서 끌어와 채워주는게 바로 interpolation이다. 사진의 경우 주변에 있는 색상들로 공백인 px을 채운다.
그라데이션도 interpolation으로 그릴 수 있다.

https://www.pinterest.co.kr/pin/760475087054803380/
우리는 맨 위에 있는 분홍색 rgba와 아래 있는 하늘색 rbga를 정확하게 안다면, interpolation이 알아서 중간 값을 찾아서 그려준다.
react-spring의 interpolation
사실 애니메이션은 시작 값을 x로, 끝나는 값을 y로 잡아서 for문으로 x값을 1씩 증가하여 y에 맞닿았을 때 종료해도 된다.
하지만 움직이는 것이 매우 부자연스러울 것이다. 이는 등속운동(균등한 속도로 움직이는 것)이라 그런 것이다.
자연스러운 움직임이라면, 처음 속도는 빨랐다가 점차 느리게 움직인다. 마치 야구선수가 공을 쳤을 때 잠시 공이 눈에 안보일 정도의 엄청난 속도로 나갔다가 점차 공의 움직임이 우리 눈에 보이고 느려지는 것처럼 말이다.
https://medium.com/motion-in-interaction/animation-principles-in-ui-design-understanding-easing-bea05243fe3
react-spring interpolation을 사용하면 자동으로 속도를 빠르게 가다 천천히 움직이게 해준다. interpolation.ts에 easing이 내장되어 있기 때문인 것 같다. (조정 가능)
extrapolate
반대로 extrapolate(보외법)는 x와 y 사이의 있는 값을 추정하는 것이 아니라, 그 외의 범위를 추정해야 한다. 그렇기 때문에 정확한 예측은 불가능하다.
만약 기존의 데이터가 1, 2, 3이었다면 그 다음에 올 값을 4, 5로 예측하겠지만 어떻게 바뀔 지 알 수 없으니 정확하다 할 수 없다.
이번에 다룬건 linear interpolation이라 간단한 축에 속하지만, 만약 입체(trilinear interpolation)에 사용한다면 꽤나 까다롭고 어느정도 수학적 지식이 필요하다.
피드백은 언제나 환영합니다!
